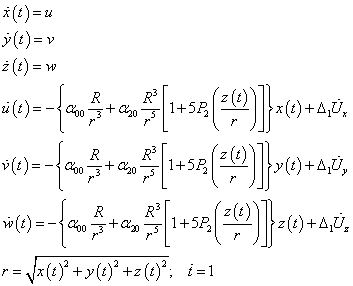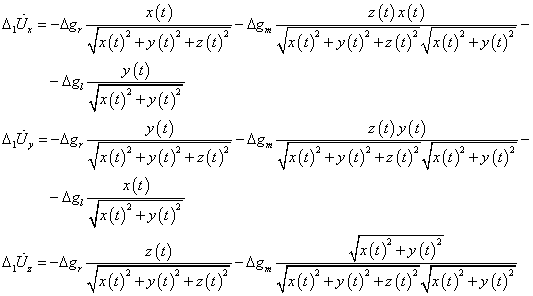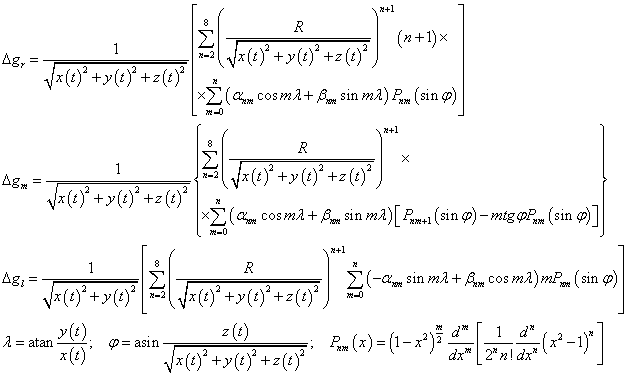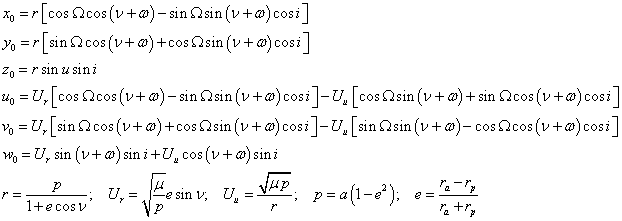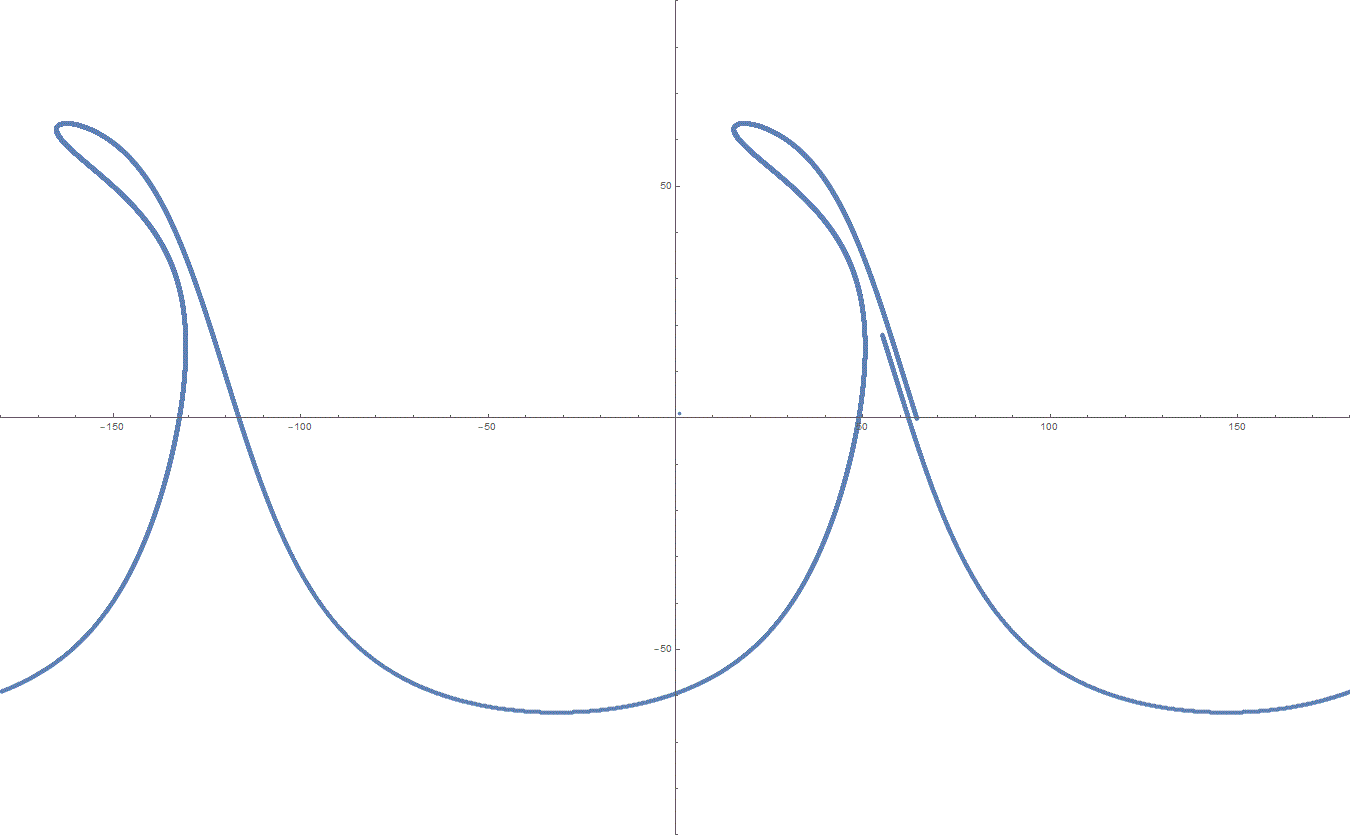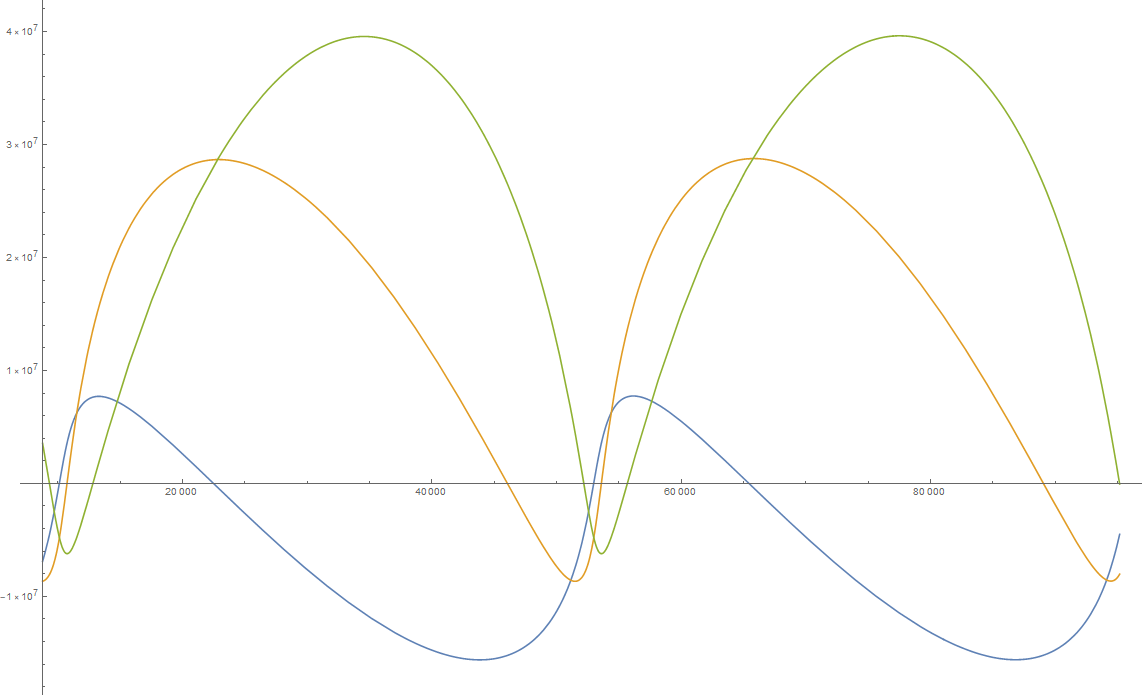Project Resonance, a Minimal HTML

Download

To propagate orbit yourself, you may wish to download the Mathematica notebook

Click me!

project resonance

Preamble

Project Resonance has been initiated to investigate interaction between waves and particles inside the inner Earth's magnetosphere. The main project goals are:

1) Exploring the dynamical characteristics of cyclotronic magnetoshperic maser

2) Studying the processes of filling in the plasma pause following magnetic disturbances

3) Outlining part of a small-scale processes witdin the global dynamics of magnetospheric plasma

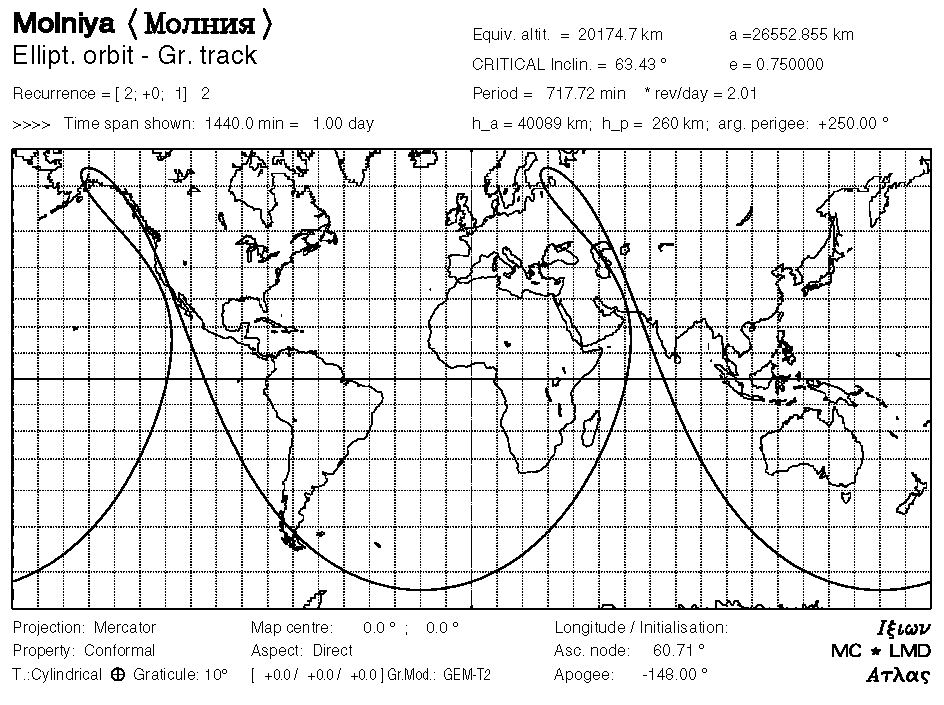
Using a GPS service by high altitude users could yield some issues related to satellite coverage. Not only is it limited but also the signal strengtd drops. However, various possibilities to navigate these satellites still exist, for example using a cross-link ranging signal or receiving a signal that is not blocked by the Earth. In case of a signal loss, possible workaround might be to navigate the satellite by means of propagating orbital (Kepler's) elements. The problem will become even more complicated and precision demanding if various perturbations are taken into account.

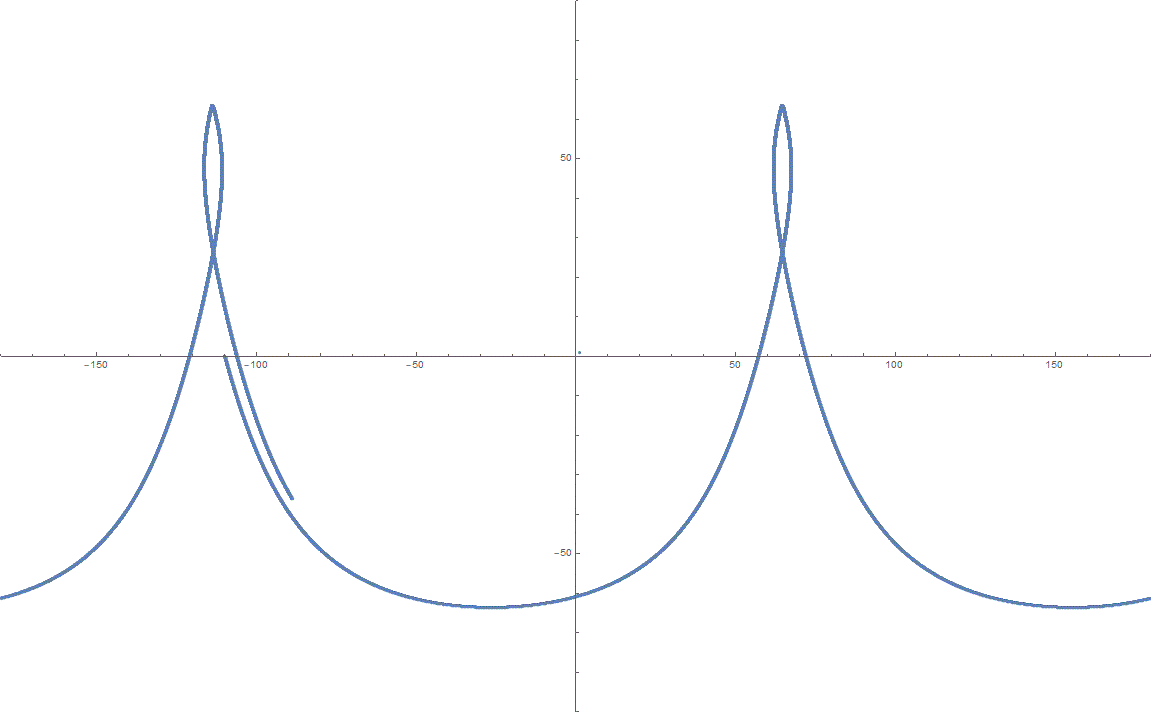
The following presentation aims at demonstrating a relatively simple algoritdm of satellite orbit propagation by solving numerically a system of first order ODEs.

A problem to be solved

The equations of motion of an artificial Earth satellite under influence of normal gravitational field expressed in ECI coordinate system have the form, [1]:

where R = 6378.388 km is the Earth equatorial radii, α00 = 62565060.5, α20 = –67905.0 are parameters of normal gravitational field of the Earth, P2 is a Legendre polynomial, and ΔUx,y,z are disturbances due to gravitational anomalies. Effects due to tdird body gravitational perturbations, solar wind pressure, and atmospheric drag are neglected.

According to [1], the gravitational disturbances are computed by following formulae:

where

In the expressions above, quantities αnm and βnm are the so-called anomaly coefficients of the JGM-3 8x8 gravitational field model. The values are listed in following table:

n	m	α	β
0	0	0.000000000000000E+000	0.000000000000000E+000
1	0	0.000000000000000E+000	0.000000000000000E+000
2	0	-1.082636022984000E-003	0.000000000000000E+000
3	0	2.532435345754400E-006	0.000000000000000E+000
4	0	1.619331205071900E-006	0.000000000000000E+000
5	0	2.277161016368800E-007	0.000000000000000E+000
6	0	-5.396484904983400E-007	0.000000000000000E+000
7	0	3.513684421031800E-007	0.000000000000000E+000
8	0	2.025187152088500E-007	0.000000000000000E+000
0	1	0.000000000000000E+000	0.000000000000000E+000
1	1	0.000000000000000E+000	0.000000000000000E+000
2	1	-2.414000052222100E-010	1.543099973784400E-009
3	1	2.192798801896500E-006	2.680118937972600E-007
4	1	-5.087253036502400E-007	-4.494599350811700E-007
5	1	-5.371651018766200E-008	-8.066346382853000E-008
6	1	-5.987797685630300E-008	2.116466435438200E-008
7	1	2.051487279767200E-007	6.936989352590800E-008
8	1	1.603458714137900E-008	4.019978159951000E-008
0	2	0.000000000000000E+000	0.000000000000000E+000
1	2	0.000000000000000E+000	0.000000000000000E+000
2	2	1.574536042767200E-006	-9.038680730186901E-007
3	2	3.090160445558300E-007	-2.114023978597500E-007
4	2	7.841223075236601E-008	1.481554569471400E-007
5	2	1.055905353867400E-007	-5.232672398763200E-008
6	2	6.012098843737300E-009	-4.650394813221700E-008
7	2	3.284490483649200E-008	9.282314388508399E-009
8	2	6.576542331674300E-009	5.381316405505600E-009
0	3	0.000000000000000E+000	0.000000000000000E+000
1	3	0.000000000000000E+000	0.000000000000000E+000
2	3	0.000000000000000E+000	0.000000000000000E+000
3	3	1.005588574145500E-007	1.972013238988900E-007
4	3	5.921574321407200E-008	-1.201129183139700E-008
5	3	-1.492615386738900E-008	-7.100877140698600E-009
6	3	1.182266411591500E-009	1.843133688062500E-010
7	3	3.528540519151200E-009	-3.061150238278800E-009
8	3	-1.946358155539900E-010	-8.723519504760500E-010
0	4	0.000000000000000E+000	0.000000000000000E+000
1	4	0.000000000000000E+000	0.000000000000000E+000
2	4	0.000000000000000E+000	0.000000000000000E+000
3	4	0.000000000000000E+000	0.000000000000000E+000
4	4	-3.982395740412900E-009	6.525605811339600E-009
5	4	-2.297912350268100E-009	3.873005077080400E-010
6	4	-3.264138911789100E-010	-1.784491334888200E-009
7	4	-5.851194914862400E-010	-2.636182215786700E-010
8	4	-3.189358021185600E-010	9.117735588725500E-011
0	5	0.000000000000000E+000	0.000000000000000E+000
1	5	0.000000000000000E+000	0.000000000000000E+000
2	5	0.000000000000000E+000	0.000000000000000E+000
3	5	0.000000000000000E+000	0.000000000000000E+000
4	5	0.000000000000000E+000	0.000000000000000E+000
5	5	4.304767504502900E-010	-1.648203946863600E-009
6	5	-2.155771151390000E-010	-4.329181698954000E-010
7	5	5.818485603087300E-013	6.397252663923500E-012
8	5	-4.615173430662800E-012	1.612520834678400E-011
0	6	0.000000000000000E+000	0.000000000000000E+000
1	6	0.000000000000000E+000	0.000000000000000E+000
2	6	0.000000000000000E+000	0.000000000000000E+000
3	6	0.000000000000000E+000	0.000000000000000E+000
4	6	0.000000000000000E+000	0.000000000000000E+000
5	6	0.000000000000000E+000	0.000000000000000E+000
6	6	2.213692555674100E-012	-5.527712220596600E-011
7	6	-2.490717682059600E-011	1.053487862926600E-011
8	6	-1.839364269763400E-012	8.627743167415000E-012
0	7	0.000000000000000E+000	0.000000000000000E+000
1	7	0.000000000000000E+000	0.000000000000000E+000
2	7	0.000000000000000E+000	0.000000000000000E+000
3	7	0.000000000000000E+000	0.000000000000000E+000
4	7	0.000000000000000E+000	0.000000000000000E+000
5	7	0.000000000000000E+000	0.000000000000000E+000
6	7	0.000000000000000E+000	0.000000000000000E+000
7	7	2.559078014987300E-014	4.475983414475100E-013
8	7	3.429761818462400E-013	3.814765668668500E-013
0	8	0.000000000000000E+000	0.000000000000000E+000
1	8	0.000000000000000E+000	0.000000000000000E+000
2	8	0.000000000000000E+000	0.000000000000000E+000
3	8	0.000000000000000E+000	0.000000000000000E+000
4	8	0.000000000000000E+000	0.000000000000000E+000
5	8	0.000000000000000E+000	0.000000000000000E+000
6	8	0.000000000000000E+000	0.000000000000000E+000
7	8	0.000000000000000E+000	0.000000000000000E+000
8	8	-1.580332289172500E-013	1.535338139714800E-013

In order to work out a numerical solution to the equations above, following initial conditions have been used in terms of orbital elements:

where μ = 3.986004415E+14 m^3/s^2. In addition, following initial orbital parameters have been given in advance:

hp = 260 km; ha = 40089 km; ω = 270 deg, Ω = 60.71 deg; i = 63.43 deg

hp = 260 km; ha = 40089 km; ω = 250 deg, Ω = 60.71 deg; i = 63.43 deg

The sub-satellite point ground track could be worked out by firstly converting the obtained results to ECF coordinate system through following formulae:

where ωE = 2π / 86164 s^–1 is the Earth angular speed and β is the Greenwich Mean Sidereal Time. Then, after some algebra, geocentric latitude and longitude of the sub-satellite point are:

where α = 1./294.978698214 is the Earth oblateness.

The Greenwich Mean Sidreal Time is computed according to recipe given in [2]

Here, MJD stands for the Modified Julian Date, i.e. the number of days since midnight on November 17th, 1858. MJD0 is at midnight between the 16th and 17th of November, 1858.

Results

The orbital elements have been propagated by means of the proposed Mathematica Notebook (see above) and compared with typical Molnia orbit ground track published in [3] for validation purposes. A full agreement is observable.

Evolution of the satellite X,Y,Z coordinates considering latter case, ECI, is visible below, so is the orbit itself.

Conclusion

Believe it or not, the orbit perturbation due to gravitational components ΔUx,y,z is more perceivable in the vicinity of perigee.

References

[1] Elyasberg, P., B. Kugaenko, V. Sinitzin, Algorithms for Estimating the Navigational Information about Satellite Position, into Russian, Moscow, Russia, Space Research Institute, Russian Academy of Sciences, 1974

[2] Montenbruck Oliver, Thomas Pfleger, Astronomy on the Personal Computer, p. 40, Springer-Verlag, 2000, ISBN 978-3-662-11187-1

[3] Capderou Michel, Satellites, Orbits, and Missions, Springer-Verlag, p. 223, 2005, ISBN : 2-287-21317-1

astodynamics

Project Resonance: Orbit Propagation